如何用定积分求三角形的面积
如何用定积分求三角形的面积
1.【引言】
在直角坐标系中,通过解析几何的知识和图形的分解,可用S=(1/2)*a*h公式来求三角形的面积,在通过学习导数及微积分之后,还可以通过微积分中的定积分知识来求三角形的面积。本文将全面介绍直角坐标系中,介绍不同形状的三角形求面积的各种方法,侧重点为定积分求面积的方法,各种方法在每道题中是否是最简单的方法要具体分析,本文将详尽两种不同的取微元的方式来求面积,目的是让读者通过总结分析,寻求最简单的一种定积分求面积的方法。
2.【定积分求面积的公式】
一般地,由上下两条连续曲线y=f2(x)与y=f1(x)以及两条直线x=a与x=b (a>b)所围成的平面图形,它的面积计算公式为:
S = ∫(b,a)[f2(x)-f1(x)]dx.
3.求不同位置三角形的面积。
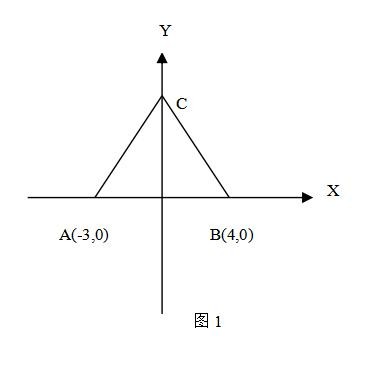
3.1.一条边AB在横坐标轴上,顶点C在纵坐标轴的正向情况:
如图1所示:已知A(-3,0),B(4,0),C(0,5)
方法一:把三角形ABC分解成两个
直角三角形OCA和OCB,用三角形的面积公式计算面积为:
S=Soca+Socb
=(1/2)*OC*OA+(1/2)*OC*OB
=(1/2)*5*3+(1/2)*5*4
=35/2平方单位。
方法二:利用微积分的知识求面积。
1.第一种方式是面积对x微元,即:ds=△ydx。
此时考虑到,由于AC,BC方程的不同,所以,对x取面积微元有两种情况,即左边的ds1=△y1dx,右边的ds2=△y2dx,三角形面积元素ds=ds1+ds2.
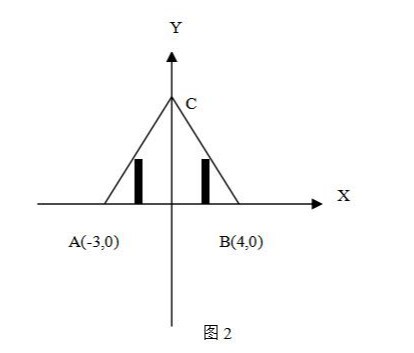
以dx为积分单元
利用直线的截距式方程,分别可以写出AC,BC的直线方程分别为:x/(-3)+y/5=1,x/4+y/5=1.即:
AC:y=5[(x/3)+1];
BC:y=5[(-x/4)+1];
x轴的方程为y=0,对于ds1:△y1=(yAC-0),所以:
ds1=5[(x/3)+1]dx,x的取值为[-3,0];同理ds2=5[(-x/4)+1]dx,x的取值为[0,4].
则三角形的面积为:
S△ABC=∫ds=∫ds1+∫ds2
=∫(-3,0) 5*[(x/3)+1]dx+∫(0,4) 5*[(-x/4)+1]dx
=5*[(x^2/6)+x][-3,0]+ 5*[(-x^2/8)+x][0,4]
=0-5*[(3/2)+(-3)]+5*[(-2)+4]-0
=15/2+10
=35/2平方单位.
注:定积分上下限本题用在小括号中,前者为下限,后者为上限,下同。
(2)定积分求面积,第二种方式,对y取面积元素,即ds=△xdy。
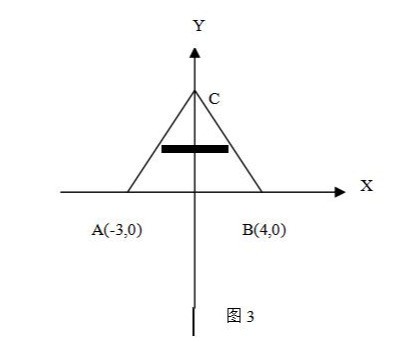
以dy为积分单元
前面已经得到AC,BC的方程为:
AC:x/(-3)+y/5=1
BC:x/4+y/5=1,此时变型为:
AC:x=3*[(y/5)-1];
BC:x=4*[1-(y/5)];
所以ds=△xdy= {4*[1-(y/5)]-3*[ (y/5)-1]}dy,y的取值为[0,5]。
则面积为:
S△ABC=∫ds
=∫(0,5){4*[1-(y/5)]-3*[ (y/5)-1]}dy
=∫(0,5)[7-(7y/5)]dy
=[7y-(7y^2/10)][0,5]
=7*5-7*5^2/10-0
=35-35/2
=35/2平方单位.
通过分析以上方法,其中方法一是初等数学方法,方法二是微积分方法。对于本题,在初等数学方法中,方法1比方法2简单,在微积分方法中,对y微元要简单一些。
综上所述,用定积分来求三角形还是其他图形的面积,要先找面积单元,面积单元有两种形式,一种面积单元是ds=△xdy,对于△x,一般是右边的函数减去左边的函数,dy是要找到积分的上下限,且上限大于下限;另一种面积单元是ds=△ydx,对于△y,一般是上面的函数减去下面的函数,dx是要找到积分的上下限,也是上限大于下限。
-

- 彭于晏也“放飞自我”了,长发造型洒脱不羁,男士留这些发型超帅
-
2026-02-04 05:37:23
-

- 牧原集团2025年北京大学优秀员工:最低月薪4万,最高达百万年薪
-
2026-02-04 05:35:08
-

- 美甲怎么剪好看,修剪方法及推圆技巧分享
-
2026-02-04 05:32:54
-

- 买房后悔了,定金能退吗?详细介绍3种情况可退定金
-
2026-02-04 05:30:40
-

- 林允儿绝美手机壁纸合集
-
2026-02-04 05:28:25
-

- 了解一下:苏轼的《黄州寒食诗帖》
-
2026-02-04 05:26:11
-

- 会穿搭就是好!“帽衫卫衣+时尚外套”=实用又不失个性
-
2026-02-04 05:23:57
-

- 佛得角共和国:非洲西岸的瑰宝
-
2026-02-04 05:21:42
-

- 敌军一日不退出国境,川军一日不返乡
-
2026-02-04 05:19:28
-

- 吕布墓在哪为何千年来无人知晓?
-
2026-02-03 07:07:31
-

- 李白是韩国人?此论让人哑然失笑,且看李白本人如何反驳这种谬论
-
2026-02-03 07:05:17
-

- 扣完五险一金,工资到手只有3500元的工作有必要坚持做下去吗?
-
2026-02-03 07:03:02
-
- 本尼迪克特·康伯巴奇 Benedict Cumberbatc
-
2026-02-03 07:00:48
-

- 中国油画院:艺术氛围感拉满,出大片的光影王国
-
2026-02-03 06:58:34
-

- 央视双胞胎姐妹花孙雨彤和孙雨朦,花式硬核科普传统节气成功出圈
-
2026-02-03 06:56:20
-

- 小科普:关于那些’外卡队‘,你或许不知道的事
-
2026-02-03 06:54:05
-

- 天津市五所、市九所和市三所
-
2026-02-03 06:51:51
-

- 泰开心之旅(十一):芭提雅富贵黄金屋
-
2026-02-03 06:49:37
-

- 山海经中的洪荒神话,存于传说中的神明
-
2026-02-03 06:47:22
-

- 捡块石头就能暴富?普通人玩转奇石收藏的三大黄金法则!
-
2026-02-03 06:45:08


 22年林立衡丈夫张清林病逝,终年80岁,副总理陶铸之女送去了花圈
22年林立衡丈夫张清林病逝,终年80岁,副总理陶铸之女送去了花圈 《越狱》演员大变样(2005-2024),时隔多年,男主现状让人惋惜
《越狱》演员大变样(2005-2024),时隔多年,男主现状让人惋惜